The Merge Sort algorithm is a sorting algorithm that is considered as an example of the divide and conquer strategy. So, in this algorithm, the array is initially divided into two equal halves and then they are combined in a sorted manner. We can think of it as a recursive algorithm that continuously splits the array in half until it cannot be further divided. If the array has multiple elements, we split the array into halves and recursively invoke the merge sort on each of the halves. Finally, when both the halves are sorted, the merge operation is applied. Merge operation is the process of taking two smaller sorted arrays and combining them to eventually make a larger one.

To know the functioning of merge sort, lets consider an array arr = {38, 27, 43, 3, 9, 82, 10}.

At first, check if the left index of array is less than the right index, if yes then calculate its mid point.

The array is {38,27,43,3,9,82,10}.Here l=left index and r=right index.

Check if l < r, then m= l+(r-1)/2.

Here l=0,r=7 and m=(0+6)/2=3.Here, we see that an array of 7 items is divided into two arrays of size 4 and 3 respectively i.e,{38,27,43,3} and {9,82,10}.

Now, again find that is left index is less than the right index for both arrays, if found yes, then again calculate mid points for both the arrays.

Now,the arrays are divided into again two arrays i.e,{38,27} , {43,3} , {9,82} and {10}.

Now, further divide these two arrays into further halves, until the atomic units of the array is reached and further division is not possible.

Now, the arrays are divided as {38},{27},{43},{3},{9},{82} and {10}.

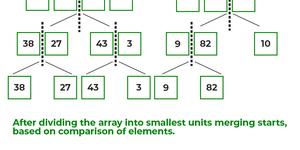
After dividing the array into smallest units, start merging the elements again based on comparison of size of elements.

Firstly, the arrays {38} and {27} get merged as {27,38}.

Next, the arrays {43} and {3} get merged as {3,43}.

Next, the arrays {9} and {82} get merged as it is {9,82}.

The array {10} will be as it is as it is a single length array.

The further merging takes place as:

Firstly, the arrays {27,38} and {3,43} get merged as {3,27,38,43}.

Next, the arrays {9,82} and {10} get merged as {9,10,82}.

The further iteration of merging is as follows:

Firstly, the arrays {3,27,38,43} and {9,10,82} get merged as {3,9,10,27,38,43,82}.

Hence, the final sorted array is {3,9,10,27,38,43,82}.


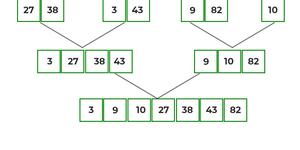
This is the working of merge sort algorithm.

Time Complexity:

The time Complexity of Merge Sort Algorithm in all three cases is same.

 1. Best Case - O(n logn)
 2. Average Case - O(n logn)
 3. Worst Case - O(n logn)

Space Complexity:

The space complexity of Merge Sort is O(n).

In merge sort all elements are copied into an auxiliary array.

So N auxiliary space is required for merge sort.