The Subset Sum Problem is all about displaying all subsets of the given array with a sum equal to a given sum. It is a variation of the 0-1 knapsack problem. In this, we have to pick items of some weight such that sum of weight of the picked items is equal to the capacity of the knapsack (x).

Now we consider the first element and now the required sum is equal to the difference between the target sum and value of first element.
The number of elements is equal to the difference between the total elements and 1.
Leave the 'first' element and now the required sum = target sum.
The number of elements is equal to the difference between the total elements and 1.

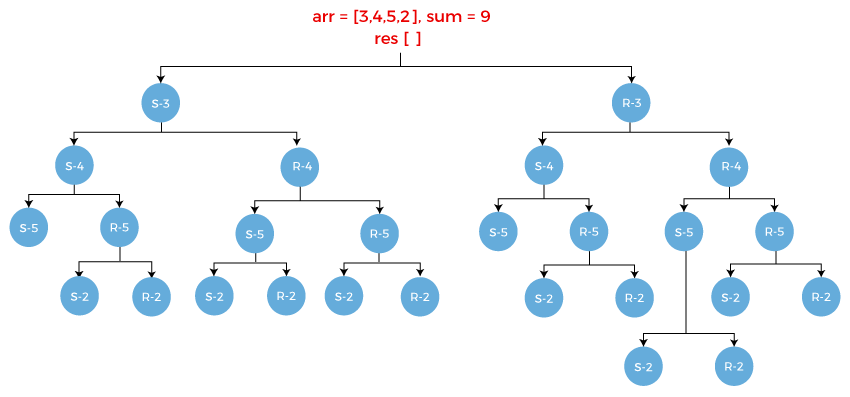
Let's understand that how can we solve the problem using recursion. Consider the array which is given below: arr = [3, 4, 5, 2]
sum = 9
result = []

In the above example, we have taken an array, and the empty array named result that stores all the values whose resultant sum is equal to 9.
First element in an array is 3. There are two scenarios:

First scenario is select. The sum is equal to the target sum - value of first element, i.e., 9 - 3 = 6 and the first element, i.e., 3 gets stored in the result array, i.e., result[].

Second scenario is reject. The array arr contains the elements 4, 5, 2, i.e., arr = [4, 5, 2] and sum would be same as 9 as we are rejecting the element 3. The result[] array would remain empty.

Now we perform the same select and reject operation on element 4 as it is the first element of the array now.

Select the element 4 from the array. Since we are selecting 4 from the array so array arr would contain the elements 5, 2, i.e., arr = [5, 2]. The sum is equal to the 6-4 = 2 and the element 4 gets stored in the result arr. The result[] = {3, 4}.

Reject the element 4 from the array. Since we are rejecting the 4 from the array so array arr would contain the elements 5, 2, i.e., arr = [5, 2]. The sum would remain same as 6 and the result array would be same as previous, i.e., {3}.

Now we perform the select and reject operation on element 5.

Select the element 5 from the array. Since we are selecting 5 from the array so array arr would contain the elements 2, i.e., arr = [2]. The sum is equal to the 2 - 5 equals to -3 and the element 5 gets stored in the result arr. The result[] = {3, 4, 5}.

Reject the element 5 from the array. Since we are rejecting 5 from the array so array arr would contain the element 2, i.e., arr = [2]. The sum would remain same as previous, i.e., 6 and the result array would be same as previous, i.e., {3, 4}.

If we observe S-5, we can see that the sum is negative that returns false. It means that there is no further subset available in the set.

Consider R-5. It also has two scenarios:

Select the element 2 from the array. Once the element 2 gets selected, the array becomes empty, i.e., arr[] = " ". The sum would be 2-2 equals to 0 and the element 2 gets stored in the result array. The result[] = [3, 4, 2].
Reject the element 2 from the array. Once the element 2 gets rejected, the array becomes empty, i.e., arr[] = " ". The sum would be same as previous, i.e., 2 and the result array would also be same as previous, i.e., [3, 4].

Consider R-4. It has two scenarios:

Select the element 5 from the array. Since we are selecting 5 from the array so array arr would contain the elements 2, i.e., arr = [2]. The sum would be 6-5 equals to 1 and the element 5 gets stored in the result array. The result[] = [3, 5].
Reject the element 5 from the array. Since we are rejecting 5 from the array so array arr would contain the element 2, i.e., arr = [2]. The sum would remain same as previous, i.e., 6 and the result array would be same as previous, i.e., {3}.

Consider S-5. It has two scenarios:

Select the element 2 from the array. Since we are selecting 2 from the array so array arr would be empty, i.e., arr = " ". The sum would be 1-2 equals to -1 and the element 2 gets stored in the result array. The result[] = [3, 5, 2].
Reject the element 2 from the array. Since we are rejecting 2 from the array so array arr would become empty. The sum would remain same as previous, i.e., 1 and the result array would be same as previous, i.e., {3, 5}.

Consider R-5. It has two scenarios:

Select the element 2 from the array. Since we are selecting 2 from the array so array arr would be empty, i.e., arr = " ". The sum would be 6-2 equals to 4 and the element 2 gets stored in the result array. The result[] = [3, 2].
Reject the element 2 from the array. Since we are rejecting 2 from the array so array arr would become empty. The sum would remain same as previous, i.e., 6 and the result array would be same as previous, i.e., {3}.

The above solution may try all subsets of given set in worst case.
Therefore time complexity of the above solution is exponential.